First Year Only Classes

Written by: Dr. Phil Hotchkiss.

In this blog, Phil Hotchkiss describes his experience in teaching a "first year only" mathematics for liberal arts course. He explains several components of his course and uses students quotes to show the positive impact on his students. In the picture to the right you can see some of the beliefs his students held on the first day of classes. It is powerful to see how they shifted!

First Year Only Classes...

“I have more drive, confidence, and abilities to actually solve the problems. Math will never be my favorite subject, but now I know I can conquer it, and that big problems aren’t as scary as they look. Math before was a very dry subject with numbers and strict answers and frustration. Math now is a creative process that is approachable. I can split up the big problems into little problems and create a route to the final answer. The satisfaction of figuring out a problem that you have been working on for over a month is amazing. This course is absolutely something I would recommend, and if you had asked me that earlier in the year, it would have been a whole other answer. I really feel as though I learned from this course, not only as a math student, but just as a student as a whole.”

This quote was from the Final Reflection assignment by one of my students in my first-year only section of my Mathematics for Liberal Arts (MLA) course this past fall (Fall 2017). It was one of several quotes from that section that spoke to me about the power of inquiry in mathematics and learning.

First-Year Only (FYO) courses at Westfield State can be offered in any discipline, are capped at 25 students and must be a 100-level course that is open to all first-year students. One of the main goals of the course is to help first-year students adjust to college life and build community. At the start of the semester, I ask my students to write a mathematical autobiography . The same student who wrote the excerpt above at the end of the semester wrote the following at the beginning of the semester:

"Math has never been my strong suit, it has always been something I have always dreaded doing. Often when faced with equations, I stare at them wishing the answer would come easy to me, but it doesn’t … I do not like math, I never have and I don’t think I ever will ... Math is scary for me when I am given an equation and I can’t remember any of the steps that I need to take to get the right answer. If I use the wrong formulas, I will get a completely wrong answer, and it is often that I forget which steps to take … My mathematical ability is sub par. It is very rare that I remember which steps to take off the top of my head."

The change exhibited by this student is what we hope will happen to all of our students in every course and were reflected in the meta-goals I had for my students in this course:

• Upon successful completion of this course, students will show improvement in recognizing and reflecting on the process of engaging in mathematical tasks;
• recognizing their mathematical abilities are not static and can improve (developing a growth mindset in mathematics) making conjectures and investigating mathematical concepts;
• persevering when struggling with a mathematical problem;
• becoming more self-monitoring, reflective learners and taking greater personal responsibility for their learning;
• reflecting on their growth as independent lifelong learners;
• appreciating mathematics as a human endeavor which is one of our most fundamental intellectual pursuits;
• understanding that mathematics is a vital, rapidly growing field of inquiry with a dedicated cohort of practitioners;
• approaching mathematics more positively and having a more balanced perspective of mathematics;
• developing an awareness of the negative impact of broadly-held societal views;
• being capable of, and interested in, considering mathematics outside of the confines of the classroom;
• recognizing, accepting and appreciating human diversity in and outside of mathematics and the mathematical contributions from these diverse populations.

Of course, this change does not happen for every student, yet in this course, I had many students write about this kind of change. I want to share with you aspects of the course (and related student reflections) that influenced this type of growth.

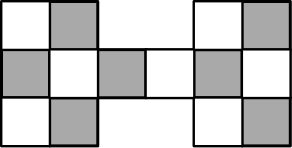
1. One of the topics we studied was the two-player game, Pennies and Paperclips, which is played on a checkered board.

Player 1 puts down two pennies on different squares.

Player 2 attempts to cover remaining squares with paperclips.  Each paperclip must cover two squares and they can only be placed horizontally or vertically. Player 2 wins if she/he is able to cover the remaining squares with the paperclips. Otherwise Player 1 wins.

While this game is relatively simple (from our perspective) and the students can easily determine the winning strategy for Player 1 (put the pennies on the same colored squares), it requires real mathematical thinking and some significant mathematics to prove why Player 2 can win when the pennies are on different colored squares. After the students worked out the proofs for both cases, I asked them to create their own boards. One student (the same student who wrote the first two quotes) created the following board:

While determining the precise conditions under which each player wins, the student was really engaged with this problem and it was exciting to see her mathematical curiosity grow.

One student reflected on this activity in her final assignment about engaging in mathematical investigations her own ability to do so:

"In the assignment of the pennies and paper clips game, it was fun to create our own boards and challenge ourselves. My classmates and I were able to come with different boards that were unique and had different patterns from one another. There was no solution to this game as it was meant to make ourselves think outside the box and interpret the board in different ways."

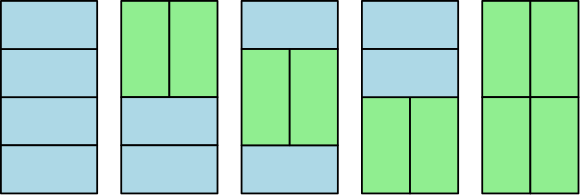
2. Another problem on which we worked was a tiling problem from combinatorics: How many ways can we tile a rectangle using rectangles? For example, if I we wish to tile a 2x4 rectangle with tiles, there are fives ways to do this:

After investigating this, the students soon discover that the sequence of the number of tilings as k increases results in the Fibonacci sequence. For us (mathematics faculty) this is easy to prove: to get the number of tilings for a rectangle, you add two vertical tiles to the top, (respectively, the bottom) of each tiling of the rectangle and add one horizontal tile to the top (respectively, the bottom) of each tiling for the . My students struggled with proving this, but eventually most were able to write up and understand the proof, see this example of student work.

One of the extra credit parts of this task was to explore the number of ways of tiling a rectangle by tiles and tiles. One student reflected on his perseverance:

"The biggest most 'break through' moment I had was at the very end, just before I wrote this out. I decided to attempt the extra-extra credit one last time, where how many times you can tile a rectangle using both and tiles. I hope I did it correctly, but i [sic] tried it over and over again and the rule seems to fit, and it makes me so happy, because I almost just gave up on it."

3. One of the assignments involved watching and reflecting on the movie Hidden Figures. I chose this movie for several reasons, obviously the mathematics is real and significant; but this past semester (Fall 2017), we had several hate crimes involving race and gender. I thought a movie involving three strong African-American women would be a good vehicle to discuss these issues with my students. After a full class period of discussing the movie and the on-campus incidents I asked my students to reflect on the movie and its connection to recent events. One student wrote the following on connections she saw between the movie and current events both on and off our campus.

"Hidden Figures has drastically impacted my perspectives on racism and sexism. The film made me realize that there were very intelligent, hard-working African-American women in NASA that did not get the recognition they deserved at the time. It also opened my eyes to how drastic the discrimination they faced was. I knew African-Americans experienced horrible racism before the Civil Rights Movement, but seeing and hearing physical examples of discrimination in the film opened my eyes to how horrible it actually was. Watching Hidden Figures made me feel bad for the women because even though they were very good mathematicians and dedicated a lot of time to their jobs they were passionate about, they received less pay, got dirty looks from their co-workers, and had to use separate restrooms and even coffee pots. Hidden Figures impacted my perspectives on recent events, both nationally and on campus, as well. Seeing the racism in the film and comparing it to the racism that exists in our world today makes me realize that even though the Civil Rights Movement occurred, we have not made much progress in changing. It breaks my heart knowing that non-white people in this world, and on campus, are experiencing hate like the three women did in Hidden Figures.

I learned many social and mathematical lessons from watching Hidden Figures. I learned that there were many African-Americans that accomplished amazing things but never got recognized for it. Although the three women from NASA eventually got recognized in Hidden Figures, there are so many non-white people that may never get recognition for their hard work. I learned that many white Americans take their privilege for granted, and it’s easy to forget that other people do not have the privileges we do. White privilege should not exist, however, since it had existed for hundreds of years, we must work together to end the discrimination once and for all. As for mathematics, I learned that there was and is a lot of sexism surrounding the mathematical field. Some men have looked down upon women who wanted to go into a mathematical or scientific field of study because women were not seen as being smart enough. However, I think as a society we need to encourage more women to enter into mathematical and scientific fields, because women can do amazing things, just like men."

4. Every year, the University selects a First-Year Read, a book that first-year students are encouraged to read. This year, the book was Visual Intelligence by Amy Herman. This book is about perception, observation and how we practice these skills can affect the way we see and interact with the world around us. The discussions about attention to detail, a willingness to consider other perspectives and thinking about what is known and not known about the situation under consideration are very connected to mathematical reasoning. One of our FYO journal assignments was to ask students to use quotes from the book to reflect on their learning. For example we used the quote: "Many people leave out what they don't know because they mistakenly think it shows ignorance or a lack of hard work. Asking the question "What don't I know?" is not the same thing as throwing out an "I don't know." In truth, what you are saying [when you ask "What don't I know?"] is, "No one right here knows and I was observant enough to notice this important fact and open it up for others to help me find the answer. " (p. 162)

One student reflected on changing from “I don’t know” to “I don’t know yet”, which is an important part of developing a growth mindset:

"I never really thought about 'I don’t know yet' versus 'I don’t know.' But, now that I think about it that is an excellent way to think about not only math but life. Mathematics is more than just doing it is working and being creative. 'I don’t know yet' makes so much more sense to say for life and mathematics. While I was frustrated working on these problems in math I never thought, 'I don’t know yet' but now I can see that I should have been thinking that way the entire time."

5. We also read the book A Mathematician’s Lament by Paul Lockhart, see this free excerpt. This book is a wonderful book about mathematics is a humanistic, creative and artistic discipline and how our current K-12 approach to mathematics education discourages students from viewing mathematics in this way. Our students identify with his perspective on mathematics education since it matches up with their own experiences. Several students used quotes from the book as prompts for reflecting on how the course changed their perception of mathematics and what it means “to do” mathematics. One student wrote:

"Through the write-ups we have done in class, reading A Mathematicians Lament, watching films in and outside of class and discussing them with each other, I have learned that the key to mathematics is how you choose to look at the problem you are given … the real 'art of mathematics' is explanation… This is [an] important lesson that I have taken away from this course. While it feels good to come up with the correct answer, that answer is not worth anything if you cannot explain to others why it is correct and how you know it is [correct]. … the real accomplishment is being able to prove your answer through your own work, which is what this course has taught, and allowed, me to do."

6. Another activity we did was watch the NOVA special The Proof about Andrew Wiles’s work on proving Fermat’s Last Theorem, see also this blog. I asked my students to reflect on how the lessons they took from the movie and our class discussion as well as what we had done in class might carry over into other courses and their field of study. One student wrote about what she had learned about the role of mistakes and perseverance in mathematics:

In relation to the video that was shown in class called 'Proof,' Andrew Wiles goes through a series of steps and learning experiences like groups in this class do, before coming to a conclusion on a proof. This involves perseverance, critical thinking, and elaboration along with colleagues or team members. Sometimes, after putting much thought and work into a problem, you realize that somewhere, a piece of information is missing, or something isn’t entirely correct. It is important to keep trying instead of giving up. Sometimes this may take awhile, and require you to walk away and come back to the problem later on (both things that Andrew Wiles does, however over many years), but it is important to keep striving. Mistakes should not be feared. Sometimes, you also need to take time into looking at methods you wouldn’t normally. You can be blind sighted by what is already known to you or what you are currently comfortable with, however, different paths and ways of seeing a problem exist and you have to utilize all sources in order to get somewhere. These are all lessons I have learned throughout this semester, and that I had noticed within the reading and video.

Conclusion:

As these quotes show, this course had a big impact on many of my students. Their reflections describe profound changes in their own perceptions of mathematics, their abilities in mathematics and their abilities to be independent learners. Watching these first-year students grow both mathematically and personally was very rewarding for me. I hope that the insights they have gained about their own learning and thinking will extend beyond this course and beyond their college studies. I will leave you with one final quote:

"I have become much more willing to start over and go back to look again. I do not think you realize how big that is. I never used to do that! Ever! If the answer was not there after I looked at the whole problem the first time, I would sit back and wait for someone else to come along and point out what the answer is and most of the time I would not even bother going back in and fixing my mistake or seeing where I went wrong. Never would I question the other answers. But that is what this class has taught me and that is what I will take away. Question everything. Keep looking. Never give up. Look in between the lines. See if you can make a connection from where you started to where you are now. Are they related? This class has changed my outlook on life and my drive for not just math, but for school. At one point, I was not even sure I wanted to go to college, just that I had to so people would not think down on me and that I had time to still figure out my future. This class has taught me much more than I have ever been taught in any other class throughout my life."