Using Inquiry for Transformative Change in Teaching

Written by: Dr. Christine von Renesse and Dr. Volker Ecke.

Many studies have already confirmed that active learning and learning with inquiry improves students’ content knowledge and learning experience. In 2016 the Conference Board of the Mathematical Sciences (CBMS) stated in “Active Learning in Post-Secondary Mathematics Education”:

A wealth of research has provided clear evidence that active learning results in better student performance and retention than more traditional, passive forms of instruction alone. Post-secondary faculty and P-12 educators have successfully used active learning methods in a diverse set of institutions and across a broad range of teaching environments. These methods have been shown to strengthen student learning and achievement in mathematics, to foster students’ confidence in their ability to do mathematics, and to increase the diversity of the mathematical community. In recognition of this, we call on institutions of higher education, mathematics departments and the mathematics faculty, public policy-makers, and funding agencies to invest time and resources to ensure that effective active learning is incorporated into post-secondary mathematics classrooms. (See also [17, 9].)

For the purpose of this blog we assume that the reader is already familiar with teaching mathematics using methods of inquiry. To learn more about our perspective on inquiry in the classroom, see our classroom page .

There is need to develop quality professional development that creates the change CBMS is calling for. Unfortunately, as Loucks-Horsley et al. write [18, p. 53]:

The fact remains that the field of education is living in a paradox of knowing one thing and doing another. For example, we say we know that learning experiences should be active, coherent, and relevant, yet too much of student learning and teacher professional development is still not interactive or reflective and remains disconnected from practice.

But changing one’s style of teaching is difficult. Guskey writes in [12]: Learning to be proficient at something new and finding meaning in a new way of doing things requires both time and effort. Any change that holds great promise for increasing teachers' competence and enhancing student learning is likely to require extra work, especially at first. The requirements of extra energy and time can significantly add to teachers' workload, even when release time is provided. [...] Furthermore, change brings a certain amount of anxiety and can be very threatening. Like practitioners in many other fields, teachers are reluctant to adopt new practices or procedures unless they feel sure they can make them work (Lortie, 1975). To change or to try something new means to risk failure. Not only would this be highly embarrassing, but it also runs counter to most teachers' strong commitment to student learning.

This blog is written in an interactive style that invites you, the reader, to make connections yourself and discover new ideas as you read and think along. Why? Because we believe that this is how learning happens best.

Concepts of Teaching

When we analyze how students learn mathematical content, we can distinguish between facts, skills (one-step procedures), methods (procedures that involve several steps) and conceptual understanding; see for example Building Conceptual Understanding in Precalculus (Greene, Porter). Of course, these categories are not fixed, in fact, procedural understanding can lead to developing methods, and with practice, methods turn into skills. Similarly, our teaching involves procedures and conceptual understanding--of teaching that is.

Activity 1:

What are your typical teaching procedures in your classroom? List at least 3. (Example: I begin class by asking the students to compare their homework)

Activity 2:

Why do you use these procedures? Give reasons grounded in the research of teaching and learning. (Example: Students make sense of the concepts more deeply when they explain their ideas to others, justify their thinking, and get confronted with new ideas that might challenge their own.)

We know that conceptual understanding is crucial for professional development. In “Facilitating Change in Undergraduate STEM Instructional Practices” Henderson et al. explain: Strategies that deliberately focus on conceptual change appear to have high levels of success in creating meaningful conceptual change in faculty that result in changes in practice (Gibbs and Coffey, 2004; Ho et al., 2001). For example, Ho et al. (2001) describe an intervention that overlaps significantly with strategies designed to promote conceptual change in students (Posner, Strike, Hewson, and Gertzog, 1982). Their process involves several steps: self-reflection (to elicit current conceptions); exposure to alternative conceptions, reflection and analysis on current conceptions (to develop dissatisfaction with current conceptions), examining examples of teaching which demonstrate more elaborated conceptions (to show that new conceptions are fruitful); and putting new conceptions into practice. (page 973)

Here are a few examples of procedures and concepts of teaching that we have discovered in our own teaching. Here is a longer (partial) list.

• Procedure: Exploration before Explanation.
  Concept: Students need to build their sense making on prior knowledge. (Note: This means learning happens differently for different students as they all have different prior knowledge. The teaching and learning has to be differentiated.)
• Procedure: Individual students present solution to the whole class. Type A: The expectation is that students present a “perfect” solution. Type B: Or, the expectation is to present the student’s current understanding, including misunderstandings, ideas, partial solutions, possible mistakes, or where they are stuck.
  Concept: For the audience: understanding and critiquing other people’s thinking, learning about alternate ways of solving a problem. For the presenter: confidence-building, taking and making constructive use of audience critiques, deepen understanding of mathematical ideas;
  Type A: Develop skill in delivering coherent, formally correct, professional presentations,
  Type B: Develop a growth mindset from working with productive mistakes.
• Procedure: Facilitating whole class discussions: the facilitator not explaining mathematical ideas, instead facilitating the students’ talking to each other.
  Concept: Mathematical authority and agency lies with the students. Whatever is happening must make sense to the students.
• Procedure: Teacher arrives in class early and sits to chat with students.
  Concept: Develop rapport with students which creates the energy in the classroom with helps students be comfortable with taking risks and sharing their thinking. Teacher gains information to better support the individual students.

We will return to these examples later in the blog.

Inquiry at the Workshop Level

Now that we have a sense of methods and procedures for teaching that we want the workshop participants to make sense of, what should an inquiry-based workshop experience look like?
We like the following definition of inquiry-based learning from Sandra Laursen et al. in [17]:

We identify IBL in post-secondary education with classroom practices that have the following characteristics:
• The main work of the course, both within and outside of class, is problem solving.
• The majority of class time is spent on student-centered activities.
• The course is driven by a carefully built sequence of investigations that guide rediscovery.
• The teacher’s role is decentralized, acting as a coach instead of a knowledge dispenser.
• Students are empowered by playing active roles - determining how class time is spent, initiating communication, and taking responsibility for learning.
• Students use reflection as well as active communication, both verbal and written, to assimilate new modes of thought, new learning strategies, and new mathematical schema.

Activity 3:

In order to reflect on components of an inquiry-based faculty workshop, read through the definition above, but substitute students with faculty and teacher with PD facilitator. What do you notice?

For us, one important insight came up around the following translation:

The PD facilitator’s role is decentralized, acting as a coach for participants instead of just dispensing the knowledge of teaching with inquiry.

Just a few years ago, we were typically tempted to just tell participants how to teach with inquiry. We were often surprised when that did not work well, especially for participants initially reluctant to changing their teaching. Later in this blog we will think more deeply about inquiry-based activities that workshop participants could do to discover concepts of teaching themselves.

In addition to concepts and procedures of teaching, even more is needed for a successful workshop, in our experience. Namely, we need to better understand the beliefs and attitudes that faculty bring to the table and work toward opening some of their assumptions about teaching and learning at an emotional, experiential level. In “Models of Faculty Development for Problem-based Learning” [16, p. 74] David Irby writes: Since faculty member’s knowledge about teaching comes from experience, new experience with the new process is required. Reading and talking about PBL are not as powerful as experiencing the method. When they experience the power of learning in this mode at an emotional level, their assumptions about teaching and learning will be challenged. This makes conceptual change possible. Notice that Problem-based learning (PBL) is very similar to IBL. The term is being used more at the high school level in the US.

So what are the beliefs, attitudes, and personal qualities of the teacher that influence the teaching process? We use the term meta goals to encompass all of these aspects.

Meta Goals for Faculty

If we accept that students need to work toward their meta-goals, faculty probably need to do the same – but what are the meta goals for faculty that are necessary for learning about teaching? Loucks-Horsley explain that [...] learning sessions should incorporate opportunities for teachers to surface and challenge their existing beliefs and assumptions and resolve conflicts that result when new ideas and practices do not fit with existing beliefs. Too often workshops, institutes, and seminars focus only on adding new skills and methods without helping teachers to understand underlying beliefs that support their use or help them know what practices they should discard as they take on new approaches. (page 266)
To explain how underlying beliefs or personality traits can influence our learning edge as teachers, we, the authors, will each share a piece of our own journey of improving our teaching.

Prof. Von’s Journey

I find that students respond better to my questions in class if I have a good rapport with them. To establish more personal connections, I try to arrive early to class to connect with students. I might ask if they need help with any of the homework but I might also ask them about their weekend, a campus event, or a political situation. It took me years to get to the point of being able to do this because I felt unsure about how to connect with American students. Between the cultural (I am German) and age difference I just didn’t know what students really cared about and I was afraid of awkward situations. I was/am also afraid about being “ridiculous” which has personal and cultural reasons. While I have made progress in making personal connections, I am now noticing that I am only connecting with some students, especially female, white students. In light of recognizing my own white privilege and prejudices, I am now working on connecting with all my students. For example, I am trying to sit with the (black and male?) students that I feel the least connected with. Trying to connect and being unsuccessful leaves me vulnerable and while I know that my vulnerability and authenticity are valuable for my teaching, it still doesn’t feel good. So what are the meta goals that I am working on? Self-awareness and reflection to notice patterns, and courage and persistence to open up to all my students.

Prof. Ecke’s Journey

In asking my students to engage in learning by inquiry, I’m asking them to make themselves vulnerable in front of the class and in front of me, the teacher. For example, for the class to productively engage in grappling with developing ideas and making sense of new concepts, I’m asking the students to share rough, early, incomplete, and possibly (maybe even likely) incorrect ideas with the whole class. This new situation often contrasts strongly with their prior experiences in mathematics classes, where incorrect answers may have led to evaluation as wrong, sometimes with an edge of shame worked in.
It has been my edge to make myself vulnerable in front of the class in authentic ways, as a way of creating a safe space for everybody in the class. This has not been easy for me, as seeming in charge and in control has been an important component in my own self-presentation, especially in professional settings, possibly though socialization messages connected to being male in this society.
It has been helpful to share stories about feeling like an impostor when I started in university, and all of a sudden, many fellow students seemed to understand so much more, and much more quickly than I did. And telling a little bit about my path to learn that depth of understanding is often of more value (in mathematics and in other areas of life) than mere speed.
A continued edge for me is finding, and choosing to take—in the moment—an opportunity for vulnerability and not-knowing (often in pedagogical classroom decisions) when it presents itself in the classroom, and resisting the urge to hide the vulnerability behind a veneer of control.

Your Journey

Activity 4:

What about you influences your teaching? Are there any meta goals you can think of that you need to work on to improve your teaching? What is in the way? Are there beliefs that are holding you back?

Here is a list of some of the meta goals for faculty that we are aware of. We suspect that there is a developmental sequence in these skills as well.

Beliefs of the teacher:

• Beliefs about learning: what is necessary to learn something?
• Beliefs about (mathematical) ability: Do all students have the ability to learn and make sense of mathematics? Is ability fixed?
• General Beliefs about students: Do I hold prejudices toward specific students?
• Beliefs about the ability to change: Can students change their thinking about mathematics? Can students change how successful they
  are in mathematics? Can students change how they learn best?
• Beliefs about teaching/facilitating: Can I change as a facilitator? Do I still teach when I don’t lecture?

Personal attributes of the teacher:

• Courage/anxiety: Is there anything you’re anxious about when teaching?
• Honesty: Do you ever lie to your students? If yes, why?
• Authenticity: Do you ever feel like you have to hide an aspect of yourself? Why do you need to hide this aspect?
• Caring about students, empathy, desire to help: Are there some students in your class you care more about than others?
• Confidence: At which times during your teaching do you feel most confident or least confident?
• Humbleness: Is there still something that you need to learn?
• Curiosity: Are you curious about student learning and students in general?
• Admitting mistakes, celebrating mistakes: How do you feel when you make a mistake in front of your class? How do you react?
• Identity (not tied to being right): How does your identity influence your teaching (including gender, race, sexual orientation, age, disabilities, nationality, native speaker, political views).
• Boundaries: How much of myself do I want to share with my students? Should there be boundaries?
• Vulnerability: Do I dare to be vulnerable with my students? If not, why not?
• Way of processing: Am I generally good at multitasking? Am I generally a fast or a slow thinker/worker?

Activity 5:

Name one new idea that emerged from the list above. How could your new idea influence your learning about teaching?

Activity 6:

Given that all faculty in a workshop have different personal qualities, how can we help them recognize and shift their beliefs and attitudes so they are ready to teach with inquiry?

Implications for Running Workshops

We believe that faculty learn about teaching just like students learn about mathematics, because the general principles of learning are independent of the content area. So let’s do another thought experiment to make this connection more explicit:
In their paper “The 5E Instructional Model: A Learning Cycle Approach for Inquiry-Based Science Teaching“, Duran and Duran describe a (not necessarily ordered) sequence for learning with inquiry:

• engage (motivation),
• explore (observing, questioning, investigating, testing predictions, and communicating),
• explain (students describe their understanding),
• elaborate (apply their new understanding), and
• evaluate (assessment, including journals).

Activity 7:

For each of these 5E-terms, think of an activity that faculty could do in a professional development setting. What do you notice?

We have been working on generating workshop activities that follow the same principles as mathematics activities for students. In the beginning of the workshop faculty need to learn what it is like to learn with inquiry. In “Teaching Practice: A Cross-Professional Perspective”, Grossman et al. explain key concepts to prepare people for professional practice:

• representations of practice,
• decomposition of practice, and
• approximations of practice.

As a representation of practice for learning with inquiry we can think of a few options:
• Theoretical description of learning with inquiry (written or spoken),
• Vignette (written excerpt from a classroom interaction),
• Video from a classroom, or
• Immersion in Inquiry (faculty are math students).

Immersion In Inquiry

Representation: We prefer to start our workshop with “immersion” in inquiry, to use Loucks-Horsley’s term [18]. In our experience, immersion quickly creates a shared understanding of learning with inquiry, and serves as a rich tool for later reflection on and decomposition of the teaching practices. As Loucks-Horsley et al. write [18, p. 43]: For fundamental change to happen, teachers need to experience learning the way they will implement it in the classroom and experiment with new behavior and gain new understandings, and that takes time. See our "IBL Workshop Video" page for some video impressions of immersion in inquiry during faculty workshops run by the authors.

We find that many of the Investigations from our "Discovering the Art of Mathematics" library for mathematics for liberal arts students are great problems for faculty immersion in inquiry. Many professors of mathematics have not learned about connections with origami, dance, music, etc. in their mathematical education, so these problems level the playing field and make for authentic inquiry. We invite all participants to be their own true mathematicians (instead of role playing a student). To ensure this, we have to be prepared to have extension questions in case a participant knows our task already or works through it very quickly. Overall, professors behave as students just like our regular students, they just work faster (see the workshop video “Supporting Group Work” on our "IBL Workshop Video" page if you haven’t done so yet). One difference we noticed is that some professors seem even more afraid than the students of “not getting it” or “not getting it right”, probably because there is more at stake, the expectations are higher, and peer pressure is on. In the language of the 5E paper, this immersion activity addresses the “engage” and “explore” stages.

Decomposition: During the reflection process we are letting the participants name the different elements of teaching practice that they noticed as well as the elements that they might have expected but that were not present. For an illustration of this reflection process, see the workshop video "Reflecting on Immersion in Inquiry" on our "IBL Workshop Video" page. In the 5E model, this corresponds to the “explain” stage. We have a list of classroom elements in mind that we want the participants to name. In our case this includes group work and name tags, supporting struggle, asking questions, staging a whole class discussion, connecting answers, talk moves, rich tasks, body language, room set up, planting successes, giving hints, etc. When participants don’t mention an item on our list, we ask specific questions to prompt them. For example, we might ask: “What is the first question the facilitator asked when we started the whole class discussion?” When they remember that the facilitator had asked participants "What did you struggle with when you worked on the mathematical problem?", we probe further by asking: “Why might we have asked this question?”

Naming elements that are not present leads often to disequilibrium, since many participants, for example, typically evaluate answers as right or wrong, or give a mini lecture at some point during their teaching. Now they wonder: Is it possible to teach without these elements? What effects did I see when the facilitator did not rely on these elements? What do I have to do instead to get to the same learning outcomes? We have often observed a transformative impact of this activity on workshop participants.

Loucks-Horsley et al. in [18, p. 70] point to features of a workshop experience that are likely to lead to transformative learning (a term they contrast with additive learning):
• Create a high level of dissonance.
• Provide sufficient time, structure, and support for teachers to think
through the dissonance experienced.
• Embed the dissonance-creating and -resolving activities in teachers
situations and practices.
• Enable teachers to develop a new repertoire of practice that fits
with their new understanding.
• Engage teachers in a continuous process of improvement.

In our experience, the “Immersion in IBL” activity touches the first three features. For the facilitator to hold the space for this dissonance requires strong tools for social-emotional support, in our experience. Given the time available in a workshop, there is need for “a continuous process of improvement” after the workshop. In the next section, we turn to the feature of “developing a new repertoire of practice that fits with their new understanding.” In Grossman's language, participants start with an "approximation of practice."

Practicing Procedures - With Concepts And Meta Goals In Mind

Activity 8:

Think of a particular procedure you would like your participants to acquire (we included a few ideas in this list). We assume that participants have discovered this procedure during the first part of the professional development. Which activity would allow them to practice this procedure while being able to reflect on their own teaching and the reasoning behind this particular procedure?

Practicing Whole Class Discussions:

In our experience from coaching in high school and higher educations classes, facilitating a productive whole class discussion is one of the most difficult skills to learn. Most facilitators are tempted to just explain the mathematical ideas, instead of eliciting student ideas, helping students listen to and disagree with each other, and helping the class to come to a common understanding.

To this effort, we developed an activity to practice some whole class discussion moves we learned from the elementary school classroom, see this blog and Chapin [20, 3]. Two participants lead a mini inquiry lesson (15-20 minutes) with all other participants being students (but also being their true mathematician selves). The leaders are supposed to just ask questions and not add their own mathematical thinking or sense making. The facilitators of the professional development are helping the leading participants if they fall back into old patterns or feel stuck in the process of facilitation.

In the reflection phase, the facilitators ask the participant leader how it felt to try these new skills. Often, powerful recognitions of underlying emotions happen: feeling out of control, not knowing how to handle a conflict between participants, struggling with not understanding a participants’ way of thinking etc. The more vulnerable the leaders dare to be, the better the reflection session for all participants. As we observe how the participants struggle with what’s in the way for them, we notice that the above mentioned meta goals (beliefs and attitudes) are really at the heart of changing a teacher’s practice. All we can do is invite them to be more self-aware and reflect on the reasons behind their choices of teacher moves.

As Gregson and Sturko state in “Teachers as Adult Learners: Reconceptualizing Professional Development”: Professional development must empower teachers through reflection and action. Learning through experience is powerful and involves a cyclical process with four stages: experience, reflection on the experience, abstract reconceptualization of the experience to consider other possibilities, and active experimentation, which leads the learner back to the first stage of the learning cycle (Kolb, 1984).
This activity is an example of the “elaboration” stage in the language of the 5E paper, as participants “apply new understanding of concepts while reinforcing new skills.”

Additional inquiry-oriented workshop activities we have created include Asking Good Questions (in a one-on-one conversation with a student, participants practice asking questions in place of providing mathematical ideas), Analyzing and Creating Assessments, Analyzing and Creating IBL Activities. If you’re curious about these activities, or would like to share, or collaborate on other workshop activities, please contact us.

Evaluation

The final stage in the 5E framework is “evaluation:” We use formative assessment during our workshops to modify and adjust our upcoming activities. This includes:
• Preparing extension questions beforehand to help us differentiate the workshop.
• Choosing which groups the second facilitator supports in more depth.
• Including/excluding specific representations of inquiry-based learning, for example additional videos.
• Regrouping participants after a break according to confidence, gender, mathematical expertise, personality, etc.
• Connecting with participants during breaks to learn about their needs and concerns. This may influence who we ask to volunteer for particular practice activities.
• Changing the workshop schedule to accommodate the needs of the group.

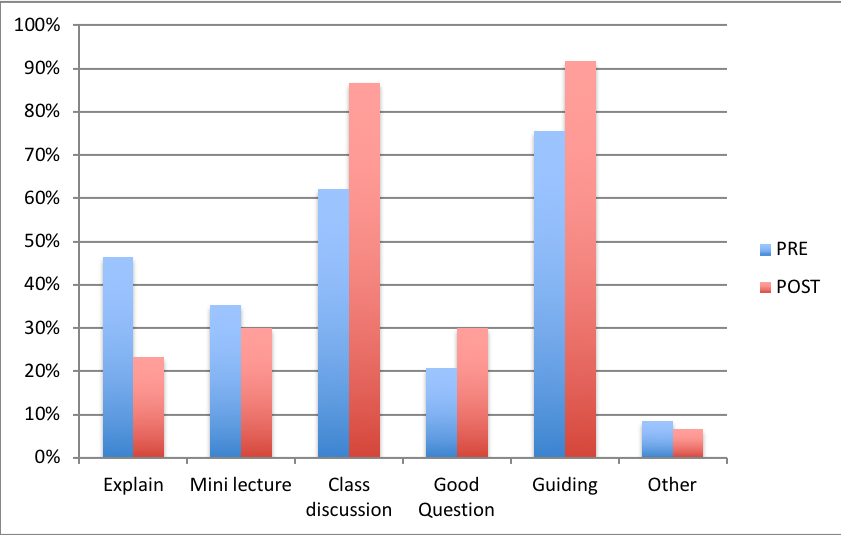
As part of the Art of Mathematics team, we collected summative data between 2012-2016 to help us improve our workshops. The following question was included in the survey to gauge a potential shift in practices:

When students in your class have misconceptions, how do you typically deal with them. Choose all that apply.
• I explain the correct answer.
• I conduct a mini-lecture about the context of the question.
• I facilitate a class discussion.
• I ask the students a good question and move on.
• I guide the students toward discovering the correct answer on their own.
• Other.

Data are available from seven traveling workshops during the 2012- 2016 period. There are 82 respondents for the PRE and 60 respondents for the POST survey. We see a shift from faculty practices centered on “telling” towards practices fostering student inquiry.

During 2016-2018, we collected 61 participant exit surveys that included the following questions:

1. Has participating in the workshop increased/decreased your interest in using inquiry in your class?
2. Has participating in the workshop increased/decreased your confidence in using inquiry in your class?

A total of 92% of the participants reported an increase in their interest and 84 % reported an increase in their confidence.
In addition, we are designing and running traveling workshops as part of the NSF project “PROfessional development Uptake through Collaborative Teams: Supporting Inquiry-Based Learning in Undergraduate Mathematics (PRODUCT, 2016-2020).” [1] Sandra Laursen’s team from “Ethnography and Evaluation Research (EER)” evaluates the ongoing traveling workshops. No detailed results have been published yet.

 

References

[2] Ballone Duran L., E. Duran, 2004. The 5E Instructional Model: A Learning Cycle Approach for Inquiry-Based Science Teaching. The Science Education Review. 40(2): 30–34.
[3] Chapin, S. H., et al. 2013 Classroom Discussions in Math : A Teacher’s Guide for Using Talk Moves to Support the Common Core and More, Grades K-6. Third edition, Sausalito, California: Math Solutions.
[5] Desimone L. M., M. S. Garet, 2015. Best Practices in Teachers Professional Development in the United States. Psychology, Society and Education. 7(3): 252–263.
[7] Erbert-May D. et al., 2011. What We Say Is Not What We Do: Effective Evaluation of Faculty Professional Development Programs. BioScience 61(7): 550–558.
[9] Freeman, S. et al. 2014. Active Learning Increases Student Performance in Science, Engineering, and Mathematics. Proceedings of the National Academy of Sciences.. 111 (23): 8410-8415. http://www.pnas.org/content/111/23/8410.full
[10] Gregson J. A., P. A. Sturko, 2007. Teachers as Adult Learners: Re-conceptualizing Professional Development. Journal of Adult Education. 36(1): 1–18.
[11] Grossman P. et al., 2009. Teaching Practice: A Cross-Professional Perspective. Teachers College Record. 111(9), 2055-2100.
[12] Guskey, T., 2002. Professional Development and Teacher Change. Teachers and Teaching: Theory and Practice 8(3-4): 381-391.
[13] Hanson P. K., L. Stultz, 2015. Collaboration-Focused Workshop for Interdisciplinary, Inter-Institutional Teams of College Science Faculty. Journal of College Science Teaching. 44(6): 30–37.
[14] Hayward C. et al., 2016. Facilitating Instructor Adoption of Inquiry- Based Learning in College Mathematics. International Journal of Research in Undergraduate Mathematics Education. 2(1): 59–82.
[15] Henderson C., A. Beach, N. Finkelstein, 2011. Facilitating Change in Undergraduate STEM Instructional Practices: An Analytic Review of the Literature. Journal of Research in Science Teaching. 48 (8): 952–984.
[16] Irby D. M., 1996. Models of Faculty Development for Problem-based Learning. Advances in Health Sciences Education. 1:69–81.
[17] Laursen, S. L., M.-L. Hassi, M. Kogan, T. J. Weston, 2014. Benefits for Women and Men of Inquiry-Based Learning in College Mathematics: A Multi-Institution Study. Journal for Research in Mathematics Education. 45(4): 406–418.
[18] Loucks-Horsley, S. et al. 2010. Designing Professional Development for Teachers of Science and Mathematics 3rd ed. Thousand Oaks, CA: Corwin Press.
[19] MAA Instructional Practices Guide https://www.maa.org/programs-and-communities/curriculum%20resources/ instructional-practices-guide.
[20] von Renesse C., V. Ecke, 2015. Inquiry-Based Learning and the Art of Mathematical Discourse. Problems, Resources, and Issues in Mathematics Undergraduate Studies 25(3): 221–37.
[21] Yoshinobu, S. 2013. Blog at Academy of Inquiry-Based Learning: Characteristics of IBL Teaching http://theiblblog.blogspot.com/2013/11/a-characteristic-of-ibl-teaching.....

Running Workshops: Resources

We have put together a page with our Resources for Running Workshops where you can access the resources we collected/created to run faculty workshops, along with brief descriptions and recommendations. These resources are based on ideas that we found in journal articles and books and on tasks that we invented. We used the tasks in many workshops to refine them and make sure that they work (for us, that is). We would love to get feedback on how they work for others to see what’s missing or could be changed.