Steven Strogatz' Reflection (Part 2)

Teaching through inquiry: A beginner’s reflections (Part 2)
by Steven Strogatz.

Read the first part of Steven’s reflections.

First Impressions

To prepare for the first class, I found it very helpful to read Volker and Chrissi’s blog post The First Class of the Semester: Setting the Stage. You should definitely take a look at that, especially if you’re considering teaching an IBL class. I followed its advice closely.

After welcoming the students and discussing what our inquiry-based classroom would be like, we jumped right into the first activity: a “gallery walk." My teaching assistant Yao Liu and I wrote nine questions on the blackboards that encircled our classroom and asked each table of students to walk around, filling in their responses to each question. The purpose of the gallery walk was to break the ice, to help the students get to know each other, and to show them that openness was welcomed and valued. It was also intended to show them that others share their attitudes, and that they are not alone. Here are some of the questions:

What are some words you would use to describe math?
Why are you taking this class?
What’s the first feeling you get when you think of math?

The responses to that last question, about the first feeling you get when you think of math – “Frustration. Pain. Satisfaction. Sick. Indifferent. Mad.” – generated a lively discussion. They gave us a chance to air some of the feelings in the room, and to knowledge that it was okay to feel them. On the other hand, there were also quite a few students who were genuinely excited about trying their hand at mathematical explorations. Many of them were younger students, freshmen and sophomores.

The others, the warier ones, were seniors who had put off fulfilling their "math and quantitative reasoning" requirement for as long as they possibly could. The only thing standing between them and graduation was this course and the swim test.

It's what you might imagine: these were students who had some unpleasant experience with math earlier in their education. For the first assignment I asked everyone to write their mathematical autobiography, detailing experiences that they had, both good and bad, in the past. I also wanted to hear about any teachers who made an impression on them, favorable or unfavorable, and what other subjects they were interested in and so on. What emerged is that even many of the seniors had liked math for several years. These were all very bright students who, somewhere along the line, had gotten discouraged.

A Surprising Reaction

Given my students’ attitudes, I was curious to see how they would take to our first mathematical activity, the same folding-and-straight-cutting challenges my colleagues and I had tackled in the workshop. Nearly everybody breezed right through the equilateral triangle and the rectangle, and there were lots of happy faces and cheerful conversations.

But what would they do with the scalene triangle? Having struggled with it myself (to say the least), I wondered whether they would be overcome by frustration.

The students were seated at tables of four, all discussing the problem, showing each other their ideas, things that had worked or not worked. After they wrestled with it for about a half-hour it turned out that only one student out of 36 was able to do it. So at the end of the class, when I noticed that there were only about five minutes left, I asked "Would you like a hint?" A few students immediately said yes, but they were quickly drowned out by the rest of the class shouting no!

I was so proud of them. They were having a true mathematical moment. That is, they were deeply engaged with a puzzle that made sense to them, and they were enjoying the struggle, and no, they did not want a hint! They were feeling what anyone who loves math feels, the pleasure of thinking. No one in the class was asking, “What is this good for?” Or "Where will I ever use this?” Those are questions that students ask only when they are not engaged.

I told the students to think about the scalene triangle over the weekend and to try it in their dorm room. Over the weekend I started to get emails from some of them expressing the excitement they felt when they solved it. One student wrote: “I am feeling exceptionally accomplished. I have to admit: this math assignment has made my day. I never thought I would ever be saying this.” From another: “I feel obligated to add a comment on my in-class progress. My original technique for solving the scalene triangle, despite my initial doubts, was in fact accurate. Moreover, I was successfully able to apply that to the irregular quadrilateral. This process of experimentation and persistence has real-world application as it demonstrates the importance of continuing a task while simultaneously approaching it in new and unusual ways. I have already learned a great deal from this class while still enjoying math, a feat I thought impossible only two weeks earlier.”

And that was how it went all semester long.

The Joy of Teaching through Inquiry

We had 27 class meetings in all, each running 75 minutes. There was no single mathematical theme to the course; my students and I felt like kids in a candy store, eager to try as many flavors as possible.

In the image above you can see the students teaching themselves the basics of group theory by striking poses of different symmetries and combining them.

A few weeks later, they investigated whether the proportions of human faces really do obey the golden ratio, as claimed in various places online (e.g., here and here) and in The DaVinci Code.

After measuring images of lots of famous faces, the students concluded that the golden ratio is not nearly as pervasive as some would have us believe. They found that there’s a lot of measurement variability, even on the same image of a given face, due to ambiguity about where to draw the lines. This was best summed up by a student who remarked, "Some of Kim Jong-un's proportions are close to the golden ratio... if you measure from his first chin."

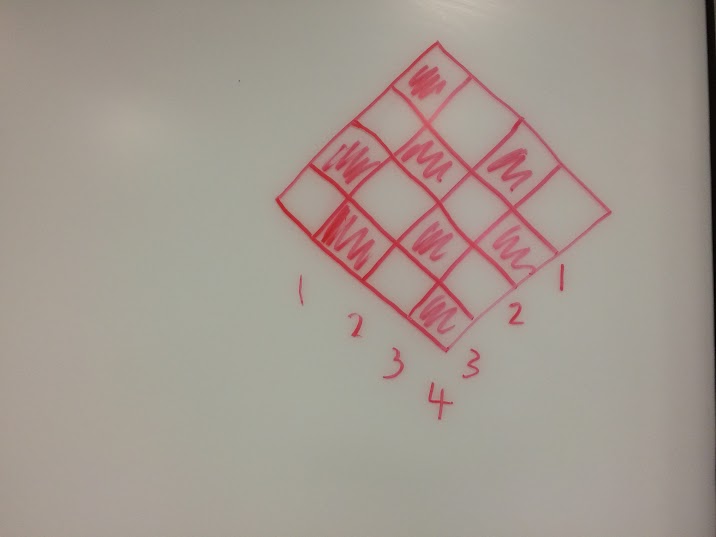
And here’s an excursion into elementary number theory, aided by Cheez-its:

Playing with the crackers led one of the students to the following “proof without words” of $1+2+3+...+n+...$ $+3+2+1=n^2$.
When he showed it to the class, everybody applauded.

 

I have to say that teaching this class was a joyful experience surpassing any other in my career. I love teaching, and I certainly love teaching students who already like math. But there’s something remarkable about working with a group of students who think they hate math or find it boring, and then seeing their surprise as they discover the beauty, pleasure, and power in it.

Additional Documents

You can download Steve Strogatz' Day-by-Day plan and his syllabus from his Fall 2014 semester.