Mathematics, Running, and Maypole Dancing
Guest blog written by:Sarah Dunn, student in the Honors Learning Community for "Mathematical Explorations" and "English Composition," Fall 2016. (Edited for blog readability by adding subheadings and classroom images.)
Mathematics and Running
If someone were to ask you to think of the math behind running where would your mind go? Would you think about speed? Would you think about the angles of your legs? I am sure there is an equation out there to calculate how to run a perfect marathon, or how to become a better runner in general using mathematics. While these are valid points of discussion and definitely have a mathematical component behind them, I am not here to talk about them. I am here to share how running and math are similar on a more fundamental level, and how they have many of the same key components.
If I were asked a year ago what math meant to me, I would say it was sitting at a desk trying to keep up with a teacher rushing through a lesson plan and trying to grasp whatever concept we were learning that day. I would picture equations that I had memorized, but could not tell you why or when to use them. However, in these short 13 weeks, my views have completely changed. I have discovered a whole new view of what mathematics really is. I have found that math is not about memorization and high test scores, that it is about self-discovery and thought process. In Honors Math 110: Math Explorations, we do just that-explore. We explore not only mathematics but also within ourselves. This class creates a bridge between math and writing; two subjects most people don’t think to pair together. Before this semester I had never thought about the importance of writing in math, or how you can apply the approaches you take to think about math to writing. Throughout the course I have learned to push myself beyond what I think I know. Every day is driven by our own curiosity. We do not learn concepts because it will be important in the future or must be squeezed in for the curriculum, but because this curiosity led us to them. “The inductive approach gives more space to observation, experimentation, and the teacher guided construction by the child of his/her own knowledge” (Ješková 559 ). In this new view of math, I have found that are many areas of overlap between running mathematics.
Community
The first similarity is community. Having a community in running is very important, in fact, ultra-marathon runner Angie Hodge claims that it is the sole reason she is still a runner today (see “Calculating Community: The Running Equation”. TEDxUNO video ). The main idea behind community is having a support group. Angie Hodge gives a lot of credit to her support team, for they are the ones who truly keep her going. Within this team, she has someone who pushes her to be better, to run faster. This person is there to challenge her to be the best she can. In my case, I do not run ultra-marathons, and I do not have a specific support group. However, I have run cross country since sixth grade, and have learned that teammates are key to success.
There will always be someone on your team who challenges you, who makes you work even harder to become a better runner. On the other hand, if you are having a bad race, and want to stop, teammates will always be there to pick you back up again. This idea of community and support directly relates to mathematics, specifically within the class we are in right now. In contrast to any other course I am in this semester, I see the people in this class every day, therefore we already have a stronger bond than any of my other classes. We are all teammates. We work together to solve conjectures and to find a common proof. There will always be someone who finds an answer first, or the next crucial idea to solving the proof. Therefore, we are constantly pushing each other to become better mathematicians. If someone is falling behind, or can’t quite fully grasp a concept, one person or sometimes even the entire class will stop what they’re doing to bring this person up to speed, to put things into different terms so that they can understand. We work as a team and do not leave anyone behind, just like a team of runners.
The Unknown
The next similarity between math and running is that the fun part is the unknown. Angie Hodge speaks about this in the aspect that she feels running is fun at times when races are unmarked, and she gets lost. I see the unknown of running differently. I think that the fun part is the not knowing what you are capable of until you do it. It is remarkable to find out what our bodies can handle and how you feel when you are running, whether its running a longer distance than you ever have before or how it feels when you finally reach a new PR. “There’s something special that happens in the ultra- marathon community, and that happens with anything that you do that is hard-that is beyond what you think your limits are” (Hodge). Not knowing if you will be able to reach a goal you have set for yourself makes it even more satisfying when you finally do. In mathematics, we are constantly looking for the unknown. We are faced with a problem and come up with our own methods and thought processes of how to find a solution. This can involve becoming active in the classroom. For example, studying maypole dancing. Every one of us thinks about the same exact questions but all of us have different thought processes. It is amazing to listen to how our own peers came to the same conclusions you did, but a completely different way. Getting inside other people’s brains is definitely a fun part of mathematics. Not knowing what you are looking for is what makes the end result so rewarding.
Mathematics in Maypole Dancing
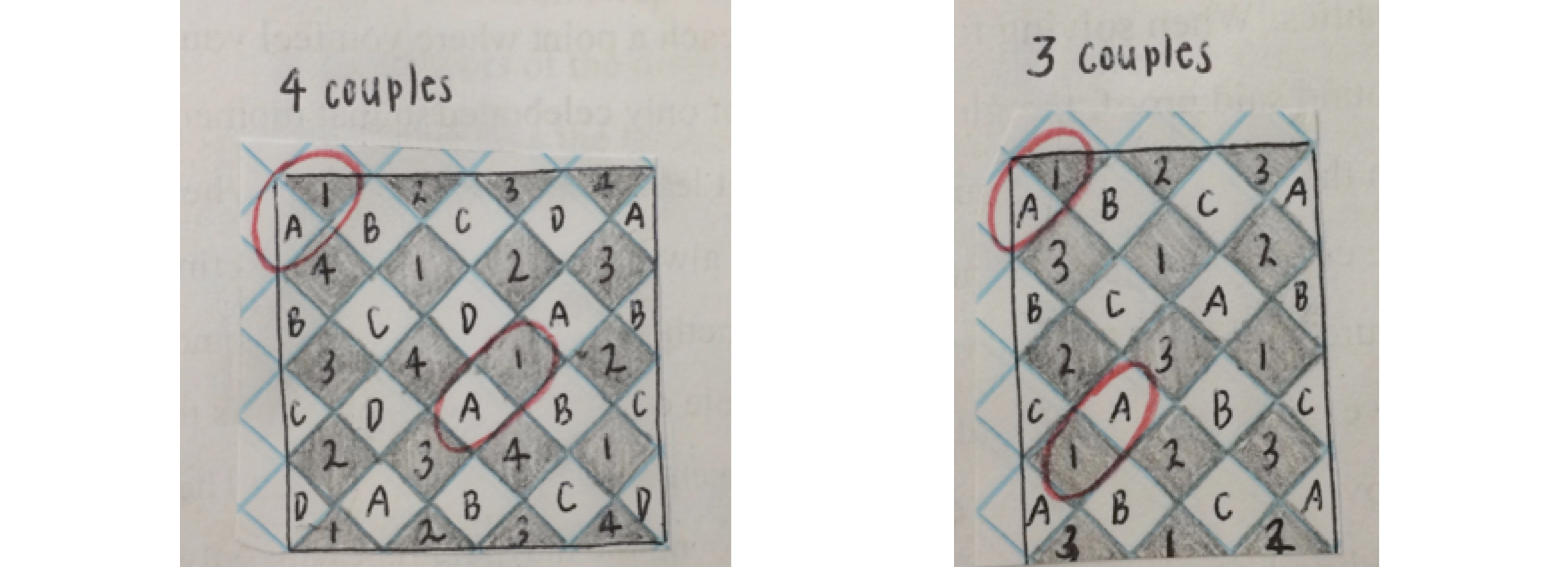
Neither running or mathematics are truly about the end result, but they are about the journey it took to get there. When running a race, and you finish with a record time, it is not solely that moment you will cherish, you will cherish and remember the work you put in to finally get there. The same goes for mathematics. When solving for proof, when you reach a point where you feel you are convinced you have found said proof, the glory of finding it is not only celebrated in that moment, rather you reflect upon the work you have put in prior to then that lead you to this moment. When solving for a proof, the end result is never known, so the focus is always on the journey. Sometimes you may study conjecture after conjecture without any idea of whether there is even a proof or not. For example, in class we are studying the math behind the Maypole dance. Our journey for this topic has been long starting over a month ago, and even still there is no endpoint in view quite yet. The first step was understanding how the dance works. We danced around the maypole first with only two colors, black and red. We first danced with 4 couples (8 ribbons) and discovered that it made a basket weave checkerboard pattern. The same pattern appeared with three couples, but something was different. Doing these two dances, we noticed that with four couples, each time we met our original partner we always did the same motions, either going over or under, meaning the pattern repeats every time they meet again. With three couples this was not the case. With three couples, each time we met out original partner, we switched motions, meaning that the pattern would not repeat until the second time we met again. Our first question to solve in our maypole journey was why the pattern repeated every time with an even number of couples, but not until the second time with an odd number of couples. We came to the conclusion that if there is an odd number of couples, for example 3: the couple begins together and we will follow the leader. The leader begins by crossing their original partner by going over, then meet a new partner and goes under, meets their last new partner by going over and then they are back to their original partner and are going under- the opposite of which they started. Repeat this process one more time, the leader meets their original partner and does the opposite motion as which they started the round, meaning this time they would go over, which is the same as the very first time they crossed each other, meaning that the pattern now repeats after the second time they meet. Pictured on the left is a picture of the pattern the dance creates with 4 couples. We see person 1 crosses over person A. These two are couple one of four. Every time these two people meet they are doing the same motions, person 1 goes over and person A goes under. On the right you will see a similar picture, however this is the pattern the dance creates with three couples. At first it may look identical until you begin to take a deeper look. The first time person 1 and person A meet, 1 is over and A is under. Then the next time these people meet in the dance, their motions have switched; person A is over and person 1 is under. The next time they meet, their movements will be opposite again, meaning that they will be the same as the first time they met, repeating the pattern on the second time they meet each other.
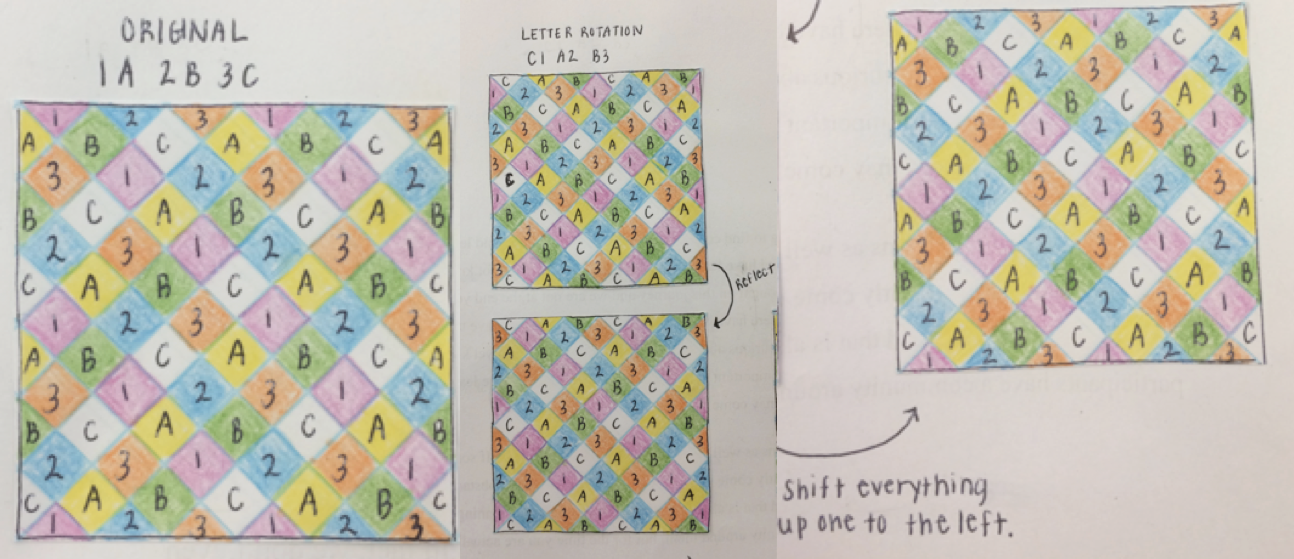
The next step of our maypole journey was learning to read patterns. Instead of dancing a pattern ourselves and knowing the dance, we were given an excel sheet of a certain pattern, and we had to find out how many people can dance it and what dance generates the pattern. From here we began to try to generate different letter (color) combinations to see which ones would generate the same pattern. This led us to discovering the letter rotation and the ribbon swap methods. The letter rotation method means that if you have a letter combination, you move either the first letter to the last spot, or the last letter to the first spot. The ribbon swap method means that you swap the order of each pair of ribbons within the combination. Sometimes by doing these methods alone, it is possible to see how the pattern may be the same as another, but sometimes we must do both methods to see the same pattern.
From here we began to look at more complex dances such as six ribbons and three colors. This dance generates a total of 729 possible patterns; however, using the letter rotation method and the ribbon swap method we know that many of them will generate the same pattern. We also know that many create the same geometric shapes, but with alternating colors. Our mission was to find out how to know how many of the 729 possibilities will actually show different patterns. Our initial thought was that there were only three. We thought this because that is the number of combinations of different color ratios; however, we disproved this because we found combinations within the same color ratio group that created different patterns.
The current spot on our journey is testing the similarities between the original pattern, the letter rotation, and the ribbon swap. Our most recent discovery is that if you draw the pattern only using letters and numbers of the original and the letter rotation, there is a way to make them create the same image. If you take the letter rotation image and reflect it, creating a mirror image of it and then move each letter and number up and left, you are given the same picture you drew as the original.
We are now trying to find conjectures about the ribbon swap and leader rotation. We are still on our maypole journey and have learned that it is okay that we may not know exactly where we are headed. We are deep in thought on this journey and we are not at the end yet. In fact, we don’t even know if there is an end. There have been so many different paths we have taken in order to understand what we were curious about in these moments. We do not yet know what we are looking for, but that is not what is important. What is important is what we have learned along our journey and to discover what else may come our way.
Passion
Both mathematicians as well as runners take on difficult tasks. If something is hard, that is okay, and both independently come up with ways to get around these obstacles. Sometimes, things take more than one try, and that is also okay. What makes math and running so similar is that both participants have a community around them, but for the time you are actually doing the math or the running, you are on your own. You are in your own mind, left to come up with your own thought process and you set goals for yourself. Both mathematicians and runners would be nowhere if their passion did not drive them to try their best. Olympic runner Steve Prefontaine once said “To give anything less than your best is to sacrifice the gift”. Those who have a passion for something will always be willing to give it their all, even if they are unsure of where their journey may take them.
Works Cited
1. Ješková Z, Lukáč S, Kireš M, et al. EFFICACY OF INQUIRY-BASED LEARNING IN MATHEMATICS, PHYSICS AND INFORMATICS IN RELATION TO THE DEVELOPMENT OF STUDENTS' INQUIRY SKILLS. Journal Of Baltic Science Education [serial online]. September 2016;15(5):559-574. Available from: Academic Search Premier, Ipswich, MA. Accessed November 29, 2016.
2. Hodge, Angie. “Calculating Community: The Running Equation”. TEDxUNO. March 16, 2015. https://www.youtube.com/watch?v=W6JG9-MWCKA&t=452s. November 29, 2016.